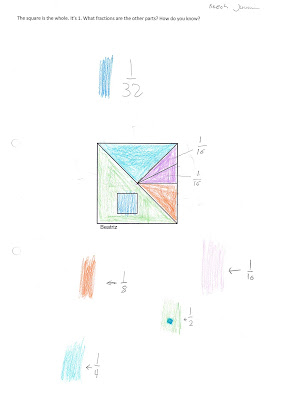
The last two posts have been about discussion that's come up in class about the fraction talk squares that two students, Beatriz and Maria, made.
They both have some interesting triangles, where the students are really not sure of the fraction. It turned out even better than I hoped because one of the students made a claim about this:
The claim went up on the Mathematical Claims Board, and we returned to it twice. (I've blogged this on the class blog too.)
I asked on Twitter:
#MTBoS, looking for a simple proof that a ▲ splits into 2 =area ▲s at a midpoint https://t.co/L9LCpmk51d @mathhombre pic.twitter.com/YgED586st7— Simon Gregg (@Simon_Gregg) March 29, 2016
And got some helpful replies, like this one from Daniel Scher:
Lovely challenge & tool: Find as many ways as you can to ÷ a ▲ into 4 equal-area ▲s @dpscher https://t.co/plthIK7Im5 pic.twitter.com/Uex1V3wrYz— Simon Gregg (@Simon_Gregg) March 29, 2016
Some people referred me to the area = 1/2 height x base rule, but this is something my class doesn't know and don't need to know yet. (It seems to me further on than the thing we're trying to prove.)
>
We also had a look at this:
This convinced a lot of the students that Maryam's claim was true.
But Miguel was still not convinced. He said:
"Technology isn't perfect. Is that really a proof?"
Yes, he really did say that! Christmas came early to 4G.
Dan Finkel suggested on Twitter that we change our triangle into a parallelogram and it will make it easier to see the truth:
We had a really good discussion about this, and quite a few students tried to persuade Miguel. There were a number of really good arguments to show how the two parts of the triangle in fact have equal areas. Hannah, for instance, suggested further splitting the pink parallelogram and the green parallelogram with their other diagonals. A lot of people thought this helped to see it.
After this, I asked the students to write about what had happened with this claim, to write what they thought about it all. Mostly great results: